MATEMÁTICAS GRADO SEXTO

                                                          AÑO LECTIVO 2019 IETIPAM 

      JORGE ELIECER GAITAN
       

-Apreciado estudiante, recuerda que  para la clase  de matemáticas cada uno  debe portar  su  materiales  para  el primer periodo. 

-A medida que se va avanzado en los temas  debes realizar  las actividades  propuestas. Las dudas   se aclararan en la  clase. 

-Al ser valorado su aprendizaje y trabajos realizados se tendrá en cuenta la rúbrica propuesta para en el primer periodo.         

No Olvidar, leer todos los apuntes ADICIONALES VISTOS Que Tienes en el cuaderno , como los mapas conceptuales del Sistema numérico, Propiedades de la suma, Multiplicación y Resolución Problemas Prácticos VISTOS en el ambiente de Aprendizaje. ingresar ¿A CADA  DIRECCIÓN  DANDO CLIC, ENCONTRARA LOS TEMAS EN EL AULA Tratados, FAVOR HACER Repaso DE ELLOS.

LIBRO GUÍA 1 DE APOYO       CARTILLA DE APOYO

 

Reflexión de Gonzalo Gallo

Consejo para estudiar 

PRIMER PERIODO

• SESIÓN 0: EVALUACIÓN DIAGNÓSTICA  Y REPASO

          1. Juegos súper  (Estrategia didáctica, Diagnóstico, Resolución de Problemas)
           
                                      

           2. Introducción a Sistemas Numéricos (arábigos, romano, binario, Maya ..)
           3 .  PROPOSICIONES 

           4 .  CONJUNTOS

           5. CONJUNTO DE LOS NÚMEROS NATURALES ( sacar fotocopia )
               5.1 Descomposición polinomio
               5.2 Orden de los Números Naturales
               5.3 Operaciones con Números Naturales
                      5.3.1   Propiedades de la Multiplicación Aplicada a Los Números Naturales
               5.4  Múltiplos
               5.5  Divisores
               5.6  Descomponer un número
               5.7  Resolución de Problemas Prácticos  (Utilizar La Guía Teórico-Práctica ).
               5.8  Ingresar la  vitutor Investigar las Propiedades de la suma, la resta,
               5.9  Calculo mental 




SESIÓN 1  NÚMEROS ENTEROS, DECIMALES, RAZONES Y PORCENTAJE
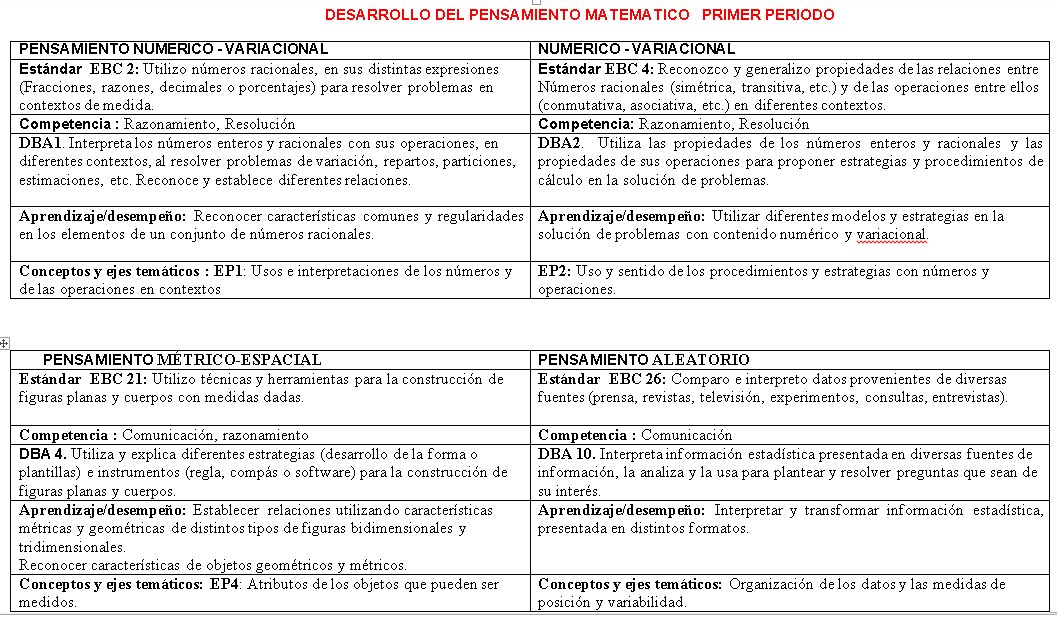
EBC 2: Utilizo números racionales, en sus distintas expresiones  (Fracciones, razones, decimales o porcentajes) para resolver problemas en contextos de medida.

              
DBA1. Interpreta los números enteros y racionales con sus operaciones, en diferentes contextos, al resolver problemas de variación, repartos, particiones, estimaciones, etc. Reconoce y establece diferentes relaciones.
              
            6.0  NÚMEROS ENTEROS 

         

             

NOTA: Dar clic a cada enunciado para ver el vídeo de  la explicación.

           6.01 Guía didáctica, trabajando con enteros para el docente guía 
           6.1 Ordenar números enteros 
           6.2 Valor absoluto de números enteros 
           6.3 Sumar y restar en la recta numérica 
           6.4 Suma y resta de números enteros 
           6.5 ¿Cómo sumar y restar  varios números enteros?
           6.6 Taller
           6.7 Juegos interactivos  
 
           7.0  LEY DE SIGNOS 
         
           8.0 Multiplicar números enteros  
           8.1 Dividir números enteros
           8.1,1 Operaciones combinadas con enteros   
           Nota : Hasta  aquí culmina el repaso de la actividad de refuerzo. 

         8.2 Potenciación de números enteros
           8.3 Eliminar signos de agrupación
           8.4 Propiedades de la potenciación 
         8.5 Propiedades de la potenciación | Producto de potencias con bases iguales
           8.6 Propiedades de la potenciación | Cociente de potencias con bases iguales 
         8.7 Propiedades de la potenciación | Potencia de una potencia 
           8.8 Propiedades de la potenciación | Potencia de un cociente o división 
         8.9 Propiedades de la potenciación | Potencias con exponentes negativos 
         8.10 Actividades interactivas - propiedades de la potenciación 
         8.11 Operaciones combinadas con números enteros 1 | Jerarquía de las operaciones 
         8.12 Operaciones combinadas con números enteros 2


        
SEGUNDO  PERIODO

                9.0  FRACCIONES  
               
          9.1  Fracciones. ¿Qué son y para qué sirven? 
            9.2   Amplificación de fracciones
          9.3  Simplificación de fracciones 
          9.4  Comparar fracciones |Gráfica o Numéricamente | mayor menor o igual 
          9.5  Suma de fracciones método gráfico 
            9.6  Suma de  fracciones 
          9.7  Resumen  suma resta multiplicación .división método gráfico 
          9.8  Juegos interactivo de operaciones con fracciones 
          9.9  Ejercicios interactivos 

        10.0  NÚMEROS DECIMALES
        10.1 ¿Qué son los números decimales? 

    

      10.2 Clasificación de los números decimales 

      10.3 Orden de los números decimales 

      10.4 ¿ Cómo ubicar en la recta numérica números decimales ?

      10.5  Suma y resta de números decimales 

      10.6  Multiplicación de números decimales 

      10.7  División de números decimales  

      10.8  Redondear números decimales 

      10.9  Convertir una fracción a decimal  1 

    10.10  Convertir fracciones a decimales 2  

    10.11  Convertir un decimal exacto a fracción 

    10.12  Convertir decimal periódico puro a fracción 

    10.13  Convertir decimal periódico mixto a fracción  

    10.14  Jugando con números decimales 

    10.15 Ejercicios Interactivos 1A Con Los Números Decimales 1 (comprueba tus Conocimientos)

    10.16  Ejercicios Interactivos 1A Con Los Números Decimales 2 (Quiero retarte  en este juego)

SESIÓN 2  NÚMEROS RACIONALES 

EBC 4: Reconozco y generalizo propiedades de las relaciones entre Números racionales (simétrica, transitiva, etc.) y de las operaciones entre ellos (conmutativa, asociativa, etc.) en diferentes contextos.

DBA2.  Utiliza las propiedades de los números enteros y racionales y las propiedades de sus operaciones para proponer estrategias y procedimientos de cálculo en la solución de problemas

DBA3. Reconoce y establece diferentes relaciones (orden y equivalencia) entre  elementos de diversos dominios numéricos y los utiliza para argumentar procedimientos sencillos.


    11.0 NÚMEROS RACIONALES
    11.1 Introducción a los números racionales | fracciones positivas o negativas 
    11.2 Orden de números  racionales 
     11.3 Orden de números racionales| Fracciones negativas    
    11.4 Ubicar en la recta numérica 
    11.5 Suma y resta de números racionales | Fracciones negativas  
    11.6 suma y resta de fracciones con diferente denominador 
    11.7 Multiplicación entre racionales por el método gráfico y analítico 
    11.8 Multiplicación de números racionales | fracciones negativas
    11.9 División de números racionales | Fracciones negativas
    11.10 Propiedades reflexiva, simétrica y transitiva de los números

    12.0  RAZONES 

     

   

13.0 PORCENTAJE 

     

SESIÓN 3 GEOMETRÍA (FIGURAS PLANAS Y CUERPOS GEOMÉTRICOS 
EBC 21: Utilizo técnicas y herramientas para la construcción de   figuras planas y cuerpos con medidas dadas.

DBA 4. Utiliza y explica diferentes estrategias (desarrollo de la forma o plantillas) e instrumentos (regla, compás o software) para la construcción de figuras planas y cuerpos.

DBA 5. Propone y  desarrolla estrategias de estimación, medición y cálculo de diferentes cantidades
(ángulos, longitudes, áreas, volúmenes, etc.) para resolver problemas.

DBA 6: Representa y  construye formas  bidimensionales y  tridimensionales con el apoyo en instrumentos de medida apropiados.

     14.0  FIGURAS PLANAS Y CUERPOS GEOMÉTRICOS 

     14.1 Conceptos Básicos en geometría (geometría, punto, RECTAS y plano)

     14.2 Trazado de perpendiculares RECTAS y Paralelas con  Regla y Compás

     14.3  Introducción a las figuras y cuerpos geométricos  

     14.4  Figuras bidimensionales 
   
     14.5  Polígonos  
     14.5.1 Clasificación de polígonos 
     14.5.2 Polígonos regulares
     14.5.3 Ángulos internos de un polígono regular
     14.5.4 Calcular el total de las diagonales de un polígono

     14.6  Geogebra: Construcción Figuras Geométricas Básicas
     14.7  Figuras geométricas tridimensionales 
      14.8  Juegos geométricos 
      14.9  Calcular Áreas de figuras  ( forma interactiva )
     14.10 Geogebra: Desarrollo de un cuerpo geométrico. 

SESIÓN 4  INTRODUCCIÓN A LA ESTADÍSTICA 
Estándar  EBC 26: Comparo e interpreto datos provenientes de diversas fuentes (prensa, revistas, televisión, experimentos, consultas, entrevistas).

DBA 10. Interpreta información estadística presentada en diversas fuentes de información, la analiza y la usa para plantear y resolver preguntas que sean de su interés.

DBA 11. Compara características compartidas por dos o más poblaciones o características
diferentes dentro de una misma población para lo cual seleccionan muestras, utiliza representaciones gráficas adecuadas y analiza los resultados obtenidos usando conjuntamente las medidas de tendencia central y el rango. 

15.0 ESTADÍSTICA 

     

       15.1 Mapa conceptual de estadística 

       15.2 Interpretación de tabla y gráficos  

       15.3 Elaboración de tabla de frecuencia 1  

       15.4 Elaboración  de tabla de frecuencia 2 

       15.5 ¿Cómo hacer una gráfica de barras? 

       15.6 ¿Cómo hacer una gráfica circular? 

       15.7 Ejercicios interactivos con diagrama de barras 

       15.8 Ejercicios interactivos con diagrama circular 

       15.9 Problema de porcentaje y diagrama 

  guía de matemáticas 1,  guía de matemáticas 2,  material didáctico 

Si ha estudiado y entendido correctamente todos estos fundamentos de grado sexto, puedo decirte que sera fácil avanzar en el los constructos Matemáticos cuando pase al siguiente Nivel.

"La verdadera Sabiduría está en reconocer la   propia ignorancia "(Sócrates )

                                             FIN

CONJUNTOS

Introdución a la Teoría de Conjuntos (Inf. Doc y/o Est.)

Conjunto 1

Conjunto 2

Conceptos bàsicos Video1 de Conjuntos (Inf. Est.) Video 2 de conjuntos ( Inf. Est.)

PROPOSICIONES

Las Proposiciones

Objetivo: Identifico y construyo proposiciones simples y reconozco el valor de verdad

Es importante el estudio de las proposiciones para los diferentes campos del conocimiento como en la investigación, la lógica digital, la factorización y análisis de circuitos lógicos, la programación de sistemas electrónicos entre otros.

Para este nivel de grado sexto daremos una breve introducción de las proposiciones en el campo de la matemática.

Que es una proposición? R/ Son expresiones lingüísticas (oraciones) de juicio y por lo general se expresa como una oración declarativa cuya característica fundamental me indica es ser verdadera o falsa pero no ambas valores a la vez.

Para representar proposiciones se usa la letras minúsculas p,q,r…entre otras por ejemplo:

p: Ocho es múltiplo de dos

q: El mes de Abril tiene 31 día

Proposiciones simples: Las proposiciones simples son aquellas que carecen de palabras de enlace como: y, o , entonces.

p: Todos los triángulos son isósceles------------; ( F )

s: 8 es un número par ---------------------------------; ( V )

Una proposición su valor de verdad se puede representar de la siguiente manera:

V o 1 o ON si la proposición es verdadera

F o 0 o OFF si la proposición es falsa

Negación de una proposición: la negación de una proposición simple se obtiene anteponiendo la palabra no es cierto que. Al negar una proposición se cambia el valor de verdad observa:

Nota : el símbolo de negación es ~ , ¬

Ejemplo: negar las siguiente proposición Simón Bolívar es el libertador y elaborar su tabla de verdad.

Respuesta:

q: Simón Bolívar es el libertador ---------------------------------> ( V )

Negando esta proposición quedaría:

~q: no es cierto que Simón Bolívar es el libertador --- > ( F )

~q: Simón Bolívar no es el libertador --- > ( F )

Tabla de verdad

Proposición	Resultado
q	V
~q	F

Concluimos que cuando q es verdadero ~q es falso y

cuando q sea falso ~q es verdadero

q	~q
V	F
F	V

Actividad 1 propuesta en esta sesión:

1) Identifica las proposiciones simples y clasifica en verdadera o falsa las frases siguientes:

a) Siete es un número natural ____________

b) ¡Lave el carro! _________________

d) Cali es la capital de la República de Colombia _______________

e) 4 x 5 = 9 ____________________

f) Todo triangulo tiene tres lados __________________

g) 3 + 9 es menor que 11 ____________

h) Los recursos renovables si se puede restaurar por procesos naturales____

i) No son recursos renovables productos derivados de los combustibles fósiles ______

J) Siéntese! ___________

k) 101 es un numero par __________

2) Escribe la negación de cada una de las proposiciones dadas en el punto 1

3) Escribe 4 frases matemáticas verdaderas

4) Escribe 4 frases matemáticas falsas

5) ¿Cómo defines una proposición?

Proposiciones compuestas y conectivos lógicos

Objetivo: Identifico y construyo proposiciones compuestas y reconozco el valor de verdad

Las proposiciones compuestas son expresiones que pueden descomponerse en otras que a su vez son proposiciones simples. Están unidas por palabras de enlace como y, o., si solo si, entonces, llamados conectivos lógicos.

Los conectivos lógicos son partículas de enlace usadas para unir dos o más proposiciones simples. En la siguiente tabla aparecen los conectivos lógicos con su nombre y símbolos.

CONECTIVO	NOMBRE	SIMBOLO
Y	Conjunción	^
O	Disyunción	V
Si … entonces	Implicación condicional	====>
…… si solo si	Doble implicación o bicondicional	<====>

La conjunción: ( ^ )

Es aquel conectivo (y) que al actúa sobre las dos o más proposiciones simples.

Para dar como respuesta el valor (V) sucede cuando las proposiciones simples que conforma la proposición compuesta son todas verdaderas de lo contrario su respuesta o resultado será (F)

Ejemplo: Se necesita una secretaria que sepa ingles y español nuevamente tenemos 4 posibilidades:

Resultado Conjunción

p	q	p ^q
F	F	F
F	V	F
V	F	F
V	V	V

p: la secretaria sabe ingles  q: la secretaria sabe español

*La secretaria no sabe ingles ni español

*La secretaria no sabe ingles y sabe español

*La secretaria sabe ingles y no sabe español

*La secretaria sabe ingles y español

La disyunción (v) :

Es aquel conectivo (o) que al actúa sobre las dos o más proposiciones simples.

Para dar como respuesta el valor (F) sucede cuando las proposiciones simples que conforma la proposición compuesta son todas falsas de lo contrario su respuesta o resultado será (V)

Ejemplo: Se necesita una secretaria que sepa ingles o español

Nuevamente tenemos 4 posibilidades:

Resultado disyunción

p	q	p V q
F	F	F
F	V	V
V	F	V
V	V	V

p: la secretaria sabe ingles q: la secretaria sabe español

*La secretaria no sabe ingles,  no sabe español

*La secretaria no sabe ingles,  si sabe español

*La secretaria sabe ingles,  no sabe español

*La secretaria sabe ingles y español

Implicación condicional:

Es aquella proposición que es falsa únicamente cuando la condición suficiente p es verdadera y la condición necesaria q es falsa. Se escribe p => q, y se lee "si p entonces q".

Ejemplo:  Si va al estadio entonces paga la boleta de entrada

p	q	p ===> q
F	F	V
F	V	V
V	F	F
V	V	V

En el enunciado el componente que está entre el "si" y el "entonces" es llamado el antecedente o el implicante y el componente que sigue a la palabra "entonces" es el consecuente o conclusión .

p = Si va al estadio (antecedente)
q = paga la boleta de entrada. ( consecuente o conclusión )

 Nota: El antecedente y el consecuente de una condicional pueden estar ligados de muchas maneras:

a: Si pongo la mano sobre el fuego, entonces me quemo (enlace causal).
b: gana el Dptvo Cali, entonces hacemos fiesta (enlace por decisión).
c: Si la carretera es recta, entonces es la distancia más corta (enlace por definición).
d: Si vienes hoy, entonces aún llegas a tiempo (enlace por circunstancia temporal).

Ejemplos: 

Si llueve entonces habrá cosecha
Si 3 es impar entonces 3 es menor que 6.
Si los cuerpos se calientan entonces se dilatan.
Me alegraría mucho, si me acompañaras.
Te llevaré al baile; si me prometes ser puntual.
Si pones atención, aprenderás más pronto.
Podría llevar dos materias, si asisto por las tardes. 

Doble Implicación :

p	q	p <===> q
F	F	V
F	V	F
V	F	F
V	V	V

La equivalencia puede reproducirse cuando en la conversación natural usan "... si y sólo si ..." o "exactamente, si". La equivalencia será cierta, si ambas oraciones tienen igual valor de certeza. Ejemplo: "El nuevo año caerá exactamente en miércoles, si la noche buena cae en martes". Las formas idiomáticas equivalentes a "... si, y sólo si, ..." son: ... sólo si..., ... únicamente si ..., sólo en el caso de que ..., ... es necesario ..., si no ..., entonces no ... .

Entonces convenimos en que "p <=> q" es cierta ( V ) solamente cuando p y q tienen el mismo valor de certeza; en los otros casos es falsa. La proposición compuesta "p <=>  q" se lee "p si y sólo si q" es la conjunción de la condicional "p <=> q" con su recíproca "<=> p"

EJEMPLOS DE PROPOSICIONES CONDICIONALES DOBLE IMPLICACIÓN:

a : Habrá cosecha si y sólo si llueve
b : Tendrás una buena calificación si y solo si respondes correctamente el examen